数据结构

链表

重要题目

6-2 有序链表合并

请编程实现有序链表合并。

函数接口定义：

1
2
3
LinkList Read( );  //按顺序依次读入元素，生成一个带头结点的单链表，表中元素值排列顺序与输入顺序一致，若输入-1，则创建链表结束（链表中不包含-1）。此处要求元素值按非递减顺序录入
LinkList Merge( LinkList L1, LinkList L2 ); 
//合并L1与L2。已知L1与L2中的元素非递减排列，要求合并后的单链表中元素也按值非递减排列。

参数 L1 和 L2 是两个有序链表（均按照非递减排列），均为带头结点的单链表。

裁判测试程序样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <stdio.h>
#include <stdlib.h>

typedef int ElemType;
typedef struct Node {
    ElemType data;
    struct Node *next;
}LNode,*LinkList;

LinkList Read( ); 
LinkList Merge( LinkList L1, LinkList L2 );

int main()
{
    LinkList L1, L2, L,p;
    L1 = Read();
    L2 = Read();
    L = Merge(L1, L2);
     if(!L)
     { 
         printf("empty");
       return 0;
     }
        p=L->next;
    while(p!=NULL){
        printf("%d ",p->data);
        p=p->next;
    }
    return 0;
}


/* 请在这里填写答案 */

输入样例：

1
2
1 3 5 8 -1
2 6 8 -1

输出样例：

1
1 2 3 5 6 8 8

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
LinkList Read( ){
    LinkList L = (LinkList)malloc(sizeof(LNode));
    L->next = NULL;
    LNode *p, *q;
    q = L;
    ElemType x;
    scanf("%d ",&x);
    while(x != -1){
        p = (LinkList)malloc(sizeof(LNode));
        p->next = NULL;
        p->data = x;
        q->next = p;
        q = p;
        scanf("%d",&x);
    }
    return L;
}

LinkList Merge( LinkList L1, LinkList L2 ){
    if(L1->next == NULL && L2->next == NULL) return NULL;   //增加一行判断语句，注意这里不能是(!L1  && !L2)，因为L1、L2在定义的时候带了头结点。
    LinkList L = (LinkList)malloc(sizeof(LNode));
    L->next = NULL;
    LinkList p = L, p1 = L1->next, p2 = L2->next;
    
    while(p1 && p2){
        if(p1->data <= p2->data){
            p->next = p1;
            p1 = p1->next;
        }
        else{
            p->next = p2;
            p2 = p2->next;
        }
        p = p->next;
    }
    p->next = p1?p1:p2;
    return L;
}
}

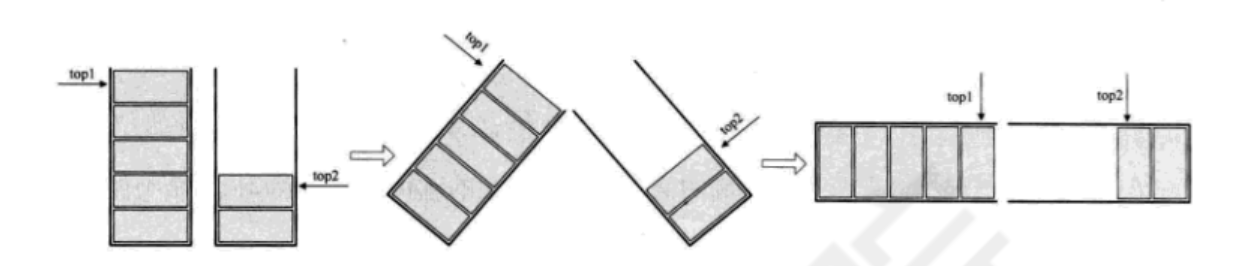
栈

一些重要知识

两栈共享

数组有两个端点，两个栈有两个栈底，让一个栈的栈底为数组的始端，即下标为0处，另一个栈为栈的末端，即下标为数组长度n-1处。这样，两个栈如果增加元素，就是两端点向中间延伸。

关键思路：它们是在数组的两端，向中间靠拢。top1和top2是栈1和栈2的栈顶指针，可以想象，只要他们俩不见面，两个栈就可以一直使用。

image-20240517152647366

重要题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
若栈采用顺序存储方式存储，现两栈共享空间V[1..m]，top[i]代表第i个栈( i =1,2)栈顶（该位置不存储对应栈数据），栈1的底在v[1]，栈2的底在V[m]，则栈满的条件是（ B ）。

A.

|top[2]-top[1]|=0

B.

top[1]-1=top[2]

C.

top[1]+top[2]=m

D.

top[1]=top[2]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
令P代表入栈，O代表出栈。则将一个字符串`3*a+b/c`变为`3 a * b c / +`的堆栈操作序列是哪个？（例如将`ABC`变成`BCA`的操作序列是PPOPOO。）  ()

A.

PPPOOOPPOPPOOO

B.

POPOPOPPOPPOOO

C.

POPPOOPPOPOOPO

D.

POPPOOPPOPPOOO

重点在于理解“变为”的意思，即是出栈的顺序，不要理解错误。

队列

复习

链队

记住初始形态，头尾指针都指着一个空节点！s

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Status InitQueue(LinkQueue &Q){
	Q.front = Q.rear = new QNode;   //开始时队头和队尾指针位于同一节点
	Q.front->next = NULL;
	return OK;
}

Status EnQueue(LinkQueue &Q, QElemType e){
    QueuePtr p;
    p = new QNode;
    p->data = e;
    p->next = NULL;
    Q.rear->next = p;
    Q.rear = p;
    return OK;
}

Status DeQueue(LinkQueue &Q, QElemType &e){
    QueuePtr p;
    if(Q.front == Q.rear)   //检测是否队空
        return ERROR;
    p = Q.front->next;   
    e = p->data;   //保留出队的元素
    Q.front->next = p->next;
    if(Q.rear == p)   //如果队尾刚好在队头后面，就把队尾移动回队头。
        Q.rear = Q.front;
    delete p;
    return OK;
}

重要题目

6-2 循环队列出队入队

分数 20

作者 YJ

单位 西南石油大学

用一个数组表示循环队列，请编写算法实现循环队列的初始化、入队和出队操作。

输入时：第一行输入队列数据空间容量，第二行依次输入5个待插入元素值，第三行再依次输入5个待插入元素值。
输出时：第一行和最后一行输出循环队列元素值及其下标（元素值（下标）），若中途出现队空或队满，则应给出相应提示。

函数接口定义：

1
2
3
void InitQ(SqQueue &Q,int N);
void AddQ(SqQueue &Q, int x );
Status DeleteQ(SqQueue &Q,int &e);

接口参数: Q是循环队列， N 是队列数组空间容量， x是入队元素， e用于接收出队元素的值

裁判测试程序样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <stdio.h>
#include <stdlib.h>
#define OK 1
#define ERROR 0
typedef int Status;
typedef struct {
  int *base;
  int front;    //队头
  int rear;    //队尾
}SqQueue;

void InitQ(SqQueue &Q,int N);
void AddQ(SqQueue &Q, int x );
Status DeleteQ(SqQueue &Q,int &e);
void printQ(SqQueue Q);  //输出队列元素及其下标位置

int N;
int main()
{
        int x,e,i;
    SqQueue Q;
        scanf("%d",&N);     //输入循环队列空间大小  
    InitQ(Q,N);
        for(i=0;i<5;i++){     
        scanf("%d",&x);
        AddQ(Q,x);
    }
    printQ(Q);   //输出队列中的各元素
    for(i=0;i<5;i++){       
        if(DeleteQ(Q,e)==OK) printf("%d is out.\n",e); 
    }
    for(i=0;i<5;i++){  
        scanf("%d",&x);
            AddQ(Q,x);
    }
    printQ(Q);
    return 0;
}
void printQ(SqQueue Q){   
    int i;
    i=Q.front;
    while(i!=Q.rear){
         printf("%d(%d) ",Q.base[i],i);
         i=(i+1)%N;
    }
    printf("\n");
}

/* 请在这里填写答案 */

输入样例1：

1
2
3
6
1 2 3 4 5
1 2 3 4 5

输出样例1：

1
2
3
4
5
6
7
1(0) 2(1) 3(2) 4(3) 5(4) 
1 is out.
2 is out.
3 is out.
4 is out.
5 is out.
1(5) 2(0) 3(1) 4(2) 5(3)

输入样例2：

1
2
3
5
1 2 3 4 5
1 2 3 4 5

输出样例2：

1
2
3
4
5
6
7
8
9
Queue Full
1(0) 2(1) 3(2) 4(3)
1 is out.
2 is out.
3 is out.
4 is out.
Queue Empty
Queue Full
1(4) 2(0) 3(1) 4(2)

代码长度限制

16 KB

时间限制

400 ms

内存限制

64 MB

错误代码示范及更正

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void InitQ(SqQueue &Q,int N){
        Q.base=(int *)malloc(N*sizeof(int));
        if(Q.base==NULL){
            return ERROR;   //1.函数开头由void定义，不能有具体的返回值，只能用return来结束。
        }
        Q.front=Q.rear=0;
       return OK;   //同1
    
}
void AddQ(SqQueue &Q, int x ){
        if((Q.rear+1)%N==Q.front){   
       return ERROR;   //同1
        }
        Q.base[Q.rear]=x;
        Q.rear=(Q.rear+1)%N;
        return OK;   //同1

    
}
Status DeleteQ(SqQueue &Q,int &e){
        if(Q.rear=Q.front){
            return ERROR;
        }
        e=Q.base[Q.front];
        Q.front=(Q.front+1)%N;
        return OK;
}

第二，观察：

image-20240513200750913

这几行的输出是题目原本代码中没定义的，需要我们加到自己写的函数之中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void InitQ(SqQueue &Q,int N){
    Q.base = (Status *)malloc(sizeof(Status));
    if(!Q.base) return;
    Q.front = Q.rear = 0;
}

void AddQ(SqQueue &Q,int x){
    if((Q.rear+1)%N == Q.front){
        printf("Queue Full\n");   //<------------------
        return;
    }
    Q.base[Q.rear] = x;
    Q.rear = (Q.rear+1)%N;
}

Status DeleteQ(SqQueue &Q,int &e){
    if(Q.front == Q.rear){
        printf("Queue Empty\n");   //<------------------
        return ERROR;
    }
    e = Q.base[Q.front];
    Q.front = (Q.front+1)%N;
    return OK;
}

串

知识

单个的字符也可以是子串（长度为1）

重要题目

1
2
3
4
5
6
7
8
9
若串S=“software”，其子串的个数是（ B ）

A. 8

B. 37

C. 36

D. 9

思路：字符串长度为8，可以有9个空，每两个空之间可以夹出一个子串，所以除空串外有：C(9,2)个子串，最后加上1个空串。

矩阵

重要题目

设有一个 10 阶的对称矩阵 A，采用压缩存储方式，以行序为主存储，a[1, 1] 为第一元素，其存储地址为 1，每个元素占一个地址空间，则 a[8, 5] 的地址为（C ）。

A. 13

B. 32

C. 33

D. 40

思路：可以等价于以a[0,0]为第一元素，则a[7,4]的地址。运用公式k = i*(i-1)/2+j-1，注意a[7,4]是第八行的第五列，所以把i=8与j=5代入即可。

image-20240628144018483

n*(n+1)/2

树

哈夫曼树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void CreatHuffmanTree(HuffmanTree &HT, int n)
{
    int m, s1, s2, i;
    if (n <= 1) return;
    m = 2 * n - 1;
    HT = new HTNode[m + 1];
    for (i = 1; i <= m; ++i)
    {
        HT[i].parent = 0;
        HT[i].lchild = 0;
        HT[i].rchild = 0;
    }
    for (i = 1; i <= n; ++i)
        cin >> HT[i].weight;
    for (i = n + 1; i <= m; ++i)
    {
        Select(HT, i - 1, s1, s2);   //选出权值小的作为s1，大的为s2
        HT[s1].parent = i;
        HT[s2].parent = i;
        HT[i].lchild = s1;   //小的给到左孩子
        HT[i].rchild = s2;
        HT[i].weight = HT[s1].weight + HT[s2].weight;
    }
}

void Select(HuffmanTree HT, int len, int &s1, int &s2)   //用于在哈夫曼树中选择两个权重最小且没有父节点的节点
{
    int i, min1 = 32767, min2 = 32767;
    for (i = 1; i <= len; i++)
    {
        if (HT[i].weight < min1 && HT[i].parent == 0)
        {
            s2 = s1;
            min2 = min1;
            min1 = HT[i].weight;
            s1 = i;
        }
        else if (HT[i].weight < min2 && HT[i].parent == 0)
        {
            min2 = HT[i].weight;
            s2 = i;
        }
    }
}

排序

直接插入排序

1
2
3
4
5
6
7
8
9
10
11
12
void InsertSort(SqList &L){
    int i,j;
    for(i=2;i<=L.length;i++){   
        if(L.r[i]>L.r[i-1]){   //遇到一组不满足顺序的元素时，选中右边的作为监视哨 
            L.r[0] = L.r[i];
            for(j=i-1;L.r[j]<L.r[0];j--){   //
                L.r[j+1] = L.r[j];
            }
            L.r[j+1] = L.r[0];
        }
    }
}